Detection of negative effective magnetic pressure instability in simulations

  • published in ApJL 740, L50 (2011),
  • by Axel Brandenburg, Koen Kemel, Nathan Kleeorin, Dhrubaditya Mitra, & Igor Rogachevskii,
  • establishes existence of negative effective magnetic pressure instability,
  • underlines a tight connection with earlier mean-field predictions.

    Background. It is generally accepted that the solar dynamo operates in the shear layer beneath the convection zone. This idea faces several difficulties that might be avoided in distributed solar dynamos shaped by near-surface shear. In that scenario, active regions would form due to large-scale (mean-field) instabilities in the near-surface shear layer. One candidate has been the negative effective magnetic pressure instability (NEMPI). Until recently, this possibility remained uncertain, because it was based on results from mean-field calculations using turbulent transport coefficients determined from direct numerical simulations (DNS). A breakthrough has now been achieved through the direct detection of this instability in simulations.

    References:

  • (BKR10) Brandenburg, A., Kleeorin, N., & Rogachevskii, I.: 2010, ``Large-scale magnetic flux concentrations from turbulent stresses,'' Astron. Nachr. 331, 5-13 (arXiv:0910.1835, ADS, DOI, PDF)

  • (BKKMR11) Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2011, ``Detection of negative effective magnetic pressure instability in turbulence simulations,'' Astrophys. J. Lett. 740, L50 (arXiv:1109.1270, DOI, HTML, PDF)

  • (BKKR12) Brandenburg, A., Kemel, K., Kleeorin, N., & Rogachevskii, I.: 2012, ``The negative effective magnetic pressure in stratified forced turbulence,'' Astrophys. J. 749, 179 (arXiv:1005.5700, ADS, DOI, PDF)

  • (BKR13) Brandenburg, A., Kleeorin, N., & Rogachevskii, I.: 2013, ``Self-assembly of shallow magnetic spots through strongly stratified turbulence,'' Astrophys. J. Lett., submitted (arXiv:1306.4915, HTML, PDF)

  • (JBKMR13) Jabbari, S., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2013, ``Surface flux concentrations in a spherical $\alpha^2$ dynamo,'' Astron. Astrophys., in press (arXiv:1302.5841, HTML)

  • (KaBKMR12) Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I.: 2012, ``Negative effective magnetic pressure in turbulent convection,'' Mon. Not. Roy. Astron. Soc. 422, 2465-2473 (arXiv:1104.4541, ADS, DOI, HTML, PDF)

  • (KBKR12) Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I.: 2012, ``Properties of the negative effective magnetic pressure instability,'' Astron. Nachr. 333, 95-100 (arXiv:1107.2752, ADS, DOI, PDF)

  • (KBKMR12) Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2012, ``Spontaneous formation of magnetic flux concentrations in stratified turbulence,'' Solar Phys. 280, 321-333 (arXiv:1112.0279, ADS, DOI, PDF)

  • (KBKMR13) Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2013, ``Active region formation through the negative effective magnetic pressure instability,'' Solar Phys., DOI: 10.1007/s11207-012-0031-8 (arXiv:1203.1232, DOI, PDF)

  • (KBKR13) Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I.: 2013, ``Nonuniformity effects in the negative effective magnetic pressure instability,'' Phys. Scr., in press (arXiv:1208.0517, HTML, PDF)

  • (LBKMR12) Losada, I. R., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2012, ``Rotational effects on the negative magnetic pressure instability,'' Astron. Astrophys. 548, A49 (arXiv:1207.5392, ADS, DOI, PDF)

  • (LBKR13) Losada, I. R., Brandenburg, A., Kleeorin, N., & Rogachevskii, I.: 2013, ``Competition of rotation and stratification in flux concentrations,'' Astron. Astrophys., in press (arXiv:1212.4077, HTML)

    Additional material

    As a result of negative effective magnetic pressure, regions with enhanced magnetic field strength must have a higher gas pressure to compensate for the negative magnetic contribution. This higher gas pressure makes these structures denser and thus heavier, so they sink! This is now seen in DNS, and is strongly reminiscent to earlier mean-field results.

    Potato sack effect in DNS for ReM=6 [animation].



    Potato sack in BKR10; for an animation, see also here.


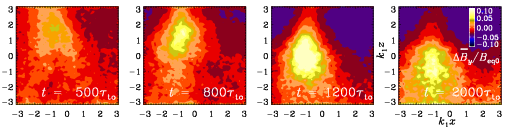
    NEMPI has now been verified for magnetic Reynolds numbers between 1 and 70. (These Reynolds numbers are based on the wavenumber of the energy-carrying eddies, which are small compared to the domain. Reynolds numbers based on the scale of the full domain are about 100 times bigger and range from 100 to 7000.) For magnetic Reynolds numbers below 1, NEMPI no longer exists. This is significant, because it explains why it has not been seen in earlier work based on quasilinear theory. Below is an example of the effective magnetic pressure as a function of the mean magnetic field, showing a minimum for field strengths below about half the equipartition value.


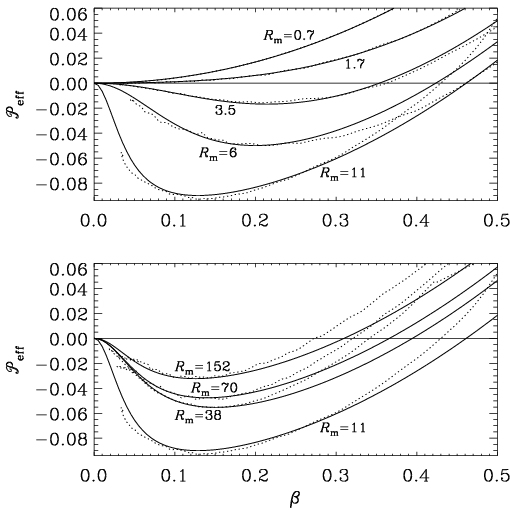
    Demonstration that ½(1-qp)B2 is negative even for a range of ReM values above ∼1.7 (for which there is still no minimum) and below ∼3.5 (for which there is).

    To be able to say something about larger values of ReM, we have to reduce the scale separation ratio. In the figure below, we show the ReM of three fit parameters βp, β*, and qp0. These parameters characterize the shape of the Peff curve (solid lines above) and fit the numerics well for weak fields (dotted lines).


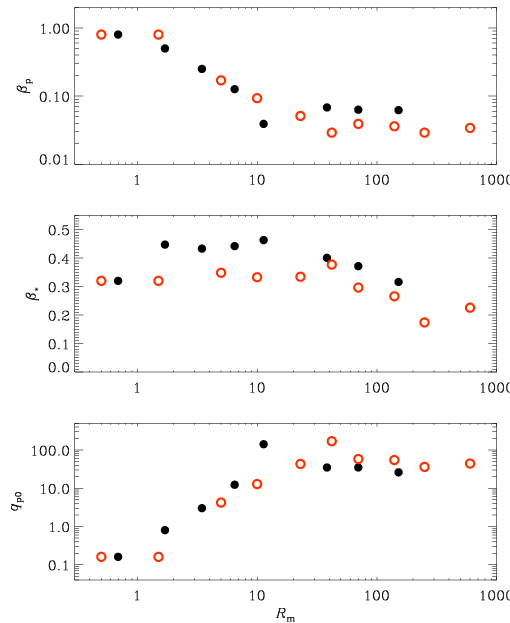
    Convergence of fit parameters βp, β*, and qp0.


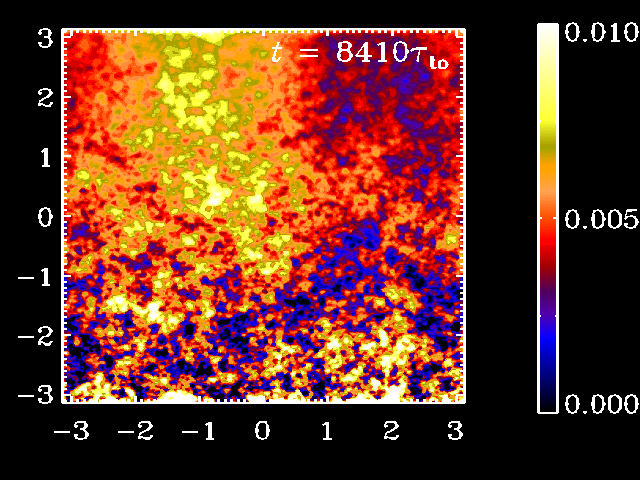
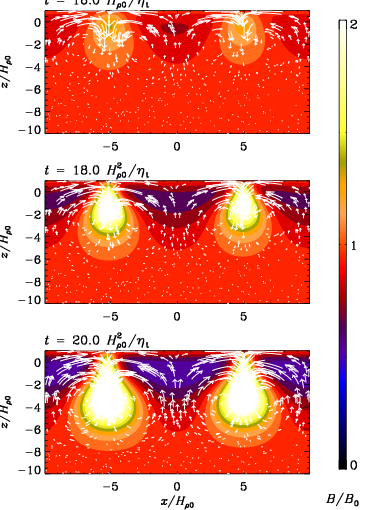
    ReM=74 with 2563 meshpoints [animation].



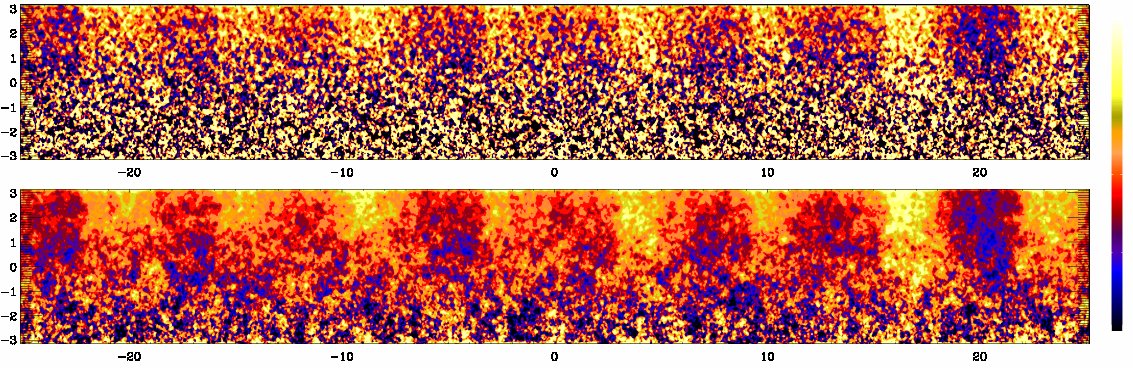
    Repetitive structures in a box that is 8 times wider, with just y averaging (upper panel) and with yt averaging (lower panel). ReM=36.


    Powerpoint presentation:

  • Detection of NEMPI in turbulence simulations (London 2012)


    $Date: 2013/06/28 05:10:34 $, $Author: brandenb $, $Revision: 1.18 $