Effective wavenumbers

cvs co public_html/teach/PencilCode/material/k_effective

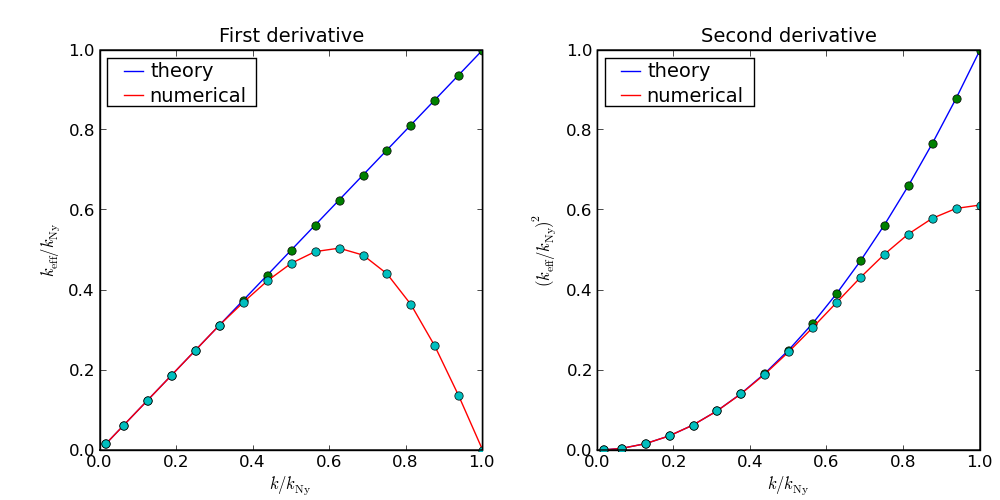
• In order to characterize the accuracy of the numerically evaluated spatial derivatives, we define effective wavenumbers k_eff. The naive way of doing it with a given code is to calculate
  
  k_eff = d/dx(coskx)/(-sinkx).
  
  
  Of course, if you are unlucky, you may end up dividing by zero. Here is how you can avoid this:
  
  
  • Define a vector A = (0, sin kx, cos kx).
  • Note that B = ∇×A = kA.
  • Evaluate numerically A.B
  • Since |A|=1 we find immediately the effective wavenumber as
    
    k_eff = <A.B>.
    
    
  In practice you could just pretend that A is the magnetic vector potential, put its amplitude to unity, and work out the magnetic helicity. This should give you k_eff. Note: in the Pencil Code, A is normalized such that A.B is equal to the input parameter amplaa=1, so |A| is not one, so we have to divide by |A|, which is printed under the name "arms".
  
  
• Next, you can do the same with the second derivatives by calculating
  
  k²_eff = <A.J>.
  
  
  where J = -∇²A, which you can pretend to be the current density.